When I first came across this problem, I was stuck. I could not write the solution in 20 minutus.
I wondered whether it should be solved by dynamic programming, or whether it should be done by 2D state variable. Or it should be done by greedy algorithm?
When I checked out the solution, I found it was fairly easy. The biggest obstable for me is how to write code by brute force, then using binary search is kind of straightforward.
The first constraint: Kolo has to eat all the piles within h hours.
We can define:
- Workable speed: Koko can eat all piles
- Unworkable speed: Koko can’t eat all piles
The second constraint: Koko would lke to eat as slow as possible. Among all the workable eating speeds, we need to find out the mininum one.
Approach 1: Brute Force
Intuition
- How do we calculate the overall time? divide and add together.
- The order by which koko eats doesn’t affect the overall times.
- Try every possible eating speed to find the smallest workable speed, incrementing it by 1 each time.
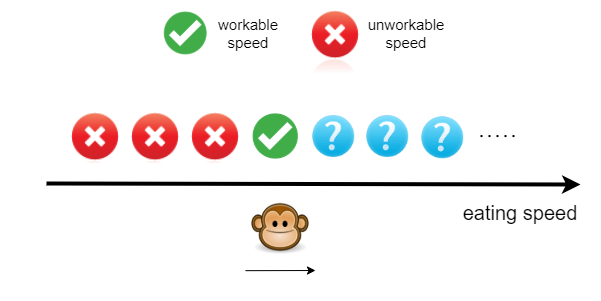
Algorithm
- Start at
speed = 1. - Given the current speed, calculate how many hours Koko needs to eat all of the piles.
- If more than
hhours, incrementspeedby 1. - if less and equal than
hhours, return thespeed.
- If more than
class Solution {
public:
bool isWorkableSpeed(const vector<int>& piles, int h, int speed)
{
int total_hour = 0;
for (const auto& pile : piles)
{
total_hour += pile / speed + (pile % speed == 0 ? 0 : 1);
if (total_hour > h) return false; // early stop
}
return true;
}
int minEatingSpeed(vector<int>& piles, int h) {
int speed = 1;
while (!isWorkableSpeed(piles, h, speed))
{
speed++;
}
return speed;
}
};
Approach 2: Binary Search
Intuition
- If speed of
nis good, then speed ofn + 1is also good. - If speed of
nis bad, then speed ofn - 1is also bad.
Algorithm
- Initialize the two boundaries of the binary search as
left = 1, right = max(piles). - Get the middle value from
leftandright. - Iterate over the piles and check if Koko can eat all the piles within
hhours givenmiddle. - If Koko can, set
right = middle, otherwise setleft = middle + 1. - If
left = right, then return it as result speed.
class Solution {
public:
bool isWorkableSpeed(const vector<int>& piles, int h, int speed)
{
int total_hour = 0;
for (const auto& pile : piles)
{
total_hour += pile / speed + (pile % speed == 0 ? 0 : 1);
if (total_hour > h) return false; // early stop
}
return true;
}
int minEatingSpeed(vector<int>& piles, int h) {
int left = 1;
int right = 1;
for (const auto& pile : piles)
{
if (right < pile) right = pile;
}
while (left < right)
{
int mid = left + ((right - left) >> 1);
if (isWorkableSpeed(piles, h, mid)) right = mid;
else left = mid + 1;
}
return right;
}
};
Summary
The problem has a structure suitable for binary search.
- A time-consuming
searchfunction. - The whole problem for searching has some kind of ordering.